L'objectif de ce projet était de nous apprendre les bases de la programmation en langage Java et par la même occasion de nous apporter un élément supplémentaire de culture informatique : les problèmes NP complets et une solution possible de résolution par les algorithmes génétiques.
Premièrement, nous avons dû implémenter un moteur générique de calcul pour
ce type de problème : gestion de la population, de la viabilité
d'un individu (fonction d'un score) et gestion des cycles de vie.
Dans un second temps, nous avons utilisé ce moteur afin de trouver des solutions acceptables aux célèbres problèmes du voyageur de commerce et du sac à dos.
Nous présenterons tout d'abord plus en détail le projet. Nous aborderons ensuite l'architecture du programme et la répartition du travail. Puis, nous détaillerons la façon dont nous avons implémenté et testé notre programme. Enfin, nous concluerons par une réflexion générale sur ce projet.
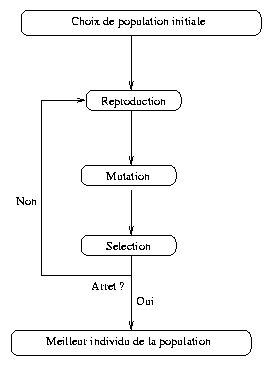
Les algorithmes génétiques, inspirés de la théorie de Darwin, permettent de tenter de résoudre des problèmes dont la solution exacte, si elle est connue, est trop longue à calculer : ce sont les problèmes NP complets (on ne connait pas de meilleur algorithme que d'essayer toutes les solutions possibles et de garder la meilleure). Voici quelques exemples d'application : problème du voyageur de commerce, du sac à dos, du dilemme du prisonnier, etc.
On crée au hasard une population initiale de solutions potentielles qui s'avèrent donc plus ou moins bonnes.
La population de solutions est alors soumise à une imitation de
l'évolution des espèces : reproduction, mutation et sélection. Les
individus se reproduisent entre eux et génèrent ainsi d'autres individus.
Puis, parmi les individus, certains, choisis aléatoirement, subissent des
mutations. Une mutation peut être vue comme un changement aléatoire d'une
caractéristique de l'individu. Finalement s'applique une sélection naturelle,
la sélection par le milieu d'évolution. Les individus les moins adaptés au
milieu disparaissent. On réitère ce procédé un certain nombre de fois et en
favorisant la survie des plus aptes
(les solutions les plus
correctes), on provoque l'apparition de meilleurs individus (Rappel :
cette remarque n'est évidemment pas absolue puisque les algorithmes
génétiques sont basés sur le hasard. Toutefois, les études empiriques sur le
sujet montrent qu'on trouve tout de même des solutions acceptables au bout
d'un nombre d'itérations suffisant
).
Ce procédé a donc pour effet que les générations successives soient de plus en plus adaptées à la résolution du problème au fur et à mesure des itérations.
Ce principe n'est pas très difficile à implémenter. En effet, la difficulté réside plutôt dans le choix des paramètres de la reproduction,de la mutation, de la sélection, du nombre d'itérations, etc..
Schéma d'illustration :

Ce mécanisme surprenant a été rigoureusement validé mathématiquement dans
les années 70. Il est ainsi prouvé qu'on arrive finalement à la meilleure
solution possible. Bien sûr, ce finalement
représente une durée qui
dépend beaucoup de la qualité de la mise en oeuvre logicielle.
Le problème du voyageur de commerce est l'un des exemples les plus connus d'application de l'algorithme génétique. L'énoncé du problème est le suivant : un voyageur de commerce doit pour son travail traverser un ensemble de N villes. Il doit toutes les traverser une fois et une seule. Le problème est de trouver le ou les chemins les plus courts qui vérifient cette contrainte.
Un autre problème de la même classe est connu sous le nom de problème
du sac à dos
(knapsack problem). On dispose d'un sac à dos de
contenance maximale (volume) N et d'un ensemble P d'éléments qu'on souhaite
ranger dans le sac, chacun de ces éléments prenant un certain volume. Selon
les contraintes citées, on souhaite remplir le sac à dos au maximum.
Nous avons décidé dès le début du projet d'utiliser CVS. Un préliminaire du travail a donc été de s'initier à cet outil qui nous a permis :
On peut critiquer l'intérêt d'utiliser CVS pour un groupe de 2 personnes seulement, mais outre l'intérêt, même seul, de conserver un historique du développement, l'objectif était aussi d'apprendre à le maîtriser pour les projets futurs où le nombre important de personnes rendra son utilisation pratiquement indispensable.
Nous avons aussi choisi d'utiliser l'EDI java Eclipse pour ses multiples aides au développement :
balises de tâches: TODO, FIXME, VERIFY, DEBUG. En effet, on peut indiquer à Eclipse quelles chaînes particulières sont utilisées pour spécifier des tâches restantes ou à surveiller, avec un niveau d'importance configurable pour chacune d'entre elles. Cette technique nous a permis de ne jamais oublier d'endroit du code où nous pouvions avoir des choses à faire, à vérifier, à corriger, etc. Elle nous a donc évidemment fait gagner un temps considérable.
Nous avons passé un certain temps à bien comprendre le sujet du projet et
à analyser les interfaces fournies avant de commencer à programmer. Puis,
nous avons réfléchi aux différentes classes à implémenter pour traiter les
différentes fonctionnalités du programme. Enfin, nous avons aussi réfléchi à
l'implémentation des méthodes clés du projet
(Individu.croisement() et Individu.mutation()) de
sorte à avoir à chaque fois la meilleure complexité possible.
Les groupes étaient tous des binômes, nous nous sommes partagé le travail de façon équitable :
Pour réaliser notre programme, nous avons réparti notre code source sur plusieurs paquetages :

Individu : la classe
Path.
Individu : la classe Fill.
Cette partie a été la plus simple à programmer. En effet, le seul rôle de
cette partie est de faire se croiser ou muter des individus choisis de façon
aléatoire et d'en sélectionner une partie à chaque itération (être donc
capable de les comparer). Les méthodes plus complexes sont évidemment plutôt
celles situées au niveau Individu.
Nous allons toutefois donner pour les classes de ce paquetage les points sur lesquels nous avons tenté d'optimiser le code.
Nous avons choisi que la liste des individus soit constamment triée. Cette liste est stockée dans une ArrayList. Choisir une des implémentations de l'interface List a été rapidement fait car les Set ne permettent par exemple pas de rajouter plusieurs fois le même élément.
Nous avons commencé par tester la LinkedList en pensant que le fait de devoir ajouter souvent des individus nous obligeait à garder une complexité correcte pour ce faire. Mais il s'est avéré que le nombre des itérations dans la liste des individus était important devant celui des ajouts (on passe en effet évidemment beaucoup de temps à parcourir la population, le plus souvent pour récupérer un objet à un index donné. Or, la récupération d'un élément est en O(1) avec une ArrayList alors qu'elle est en O(n) avec une LinkedList...).
Dans le point précédent, on explique que la liste est toujours
triée. Ce n'est pas tout à fait vrai en réalité : une petite
entorse a ce principe a été faite dans la méthode add().
Cette méthode a été modifiée pour fonctionner avec une ArrayList
Lorsque nous fonctionnions avec une LinkedList, nous effectuions
toujours l'insertion au bon endroit. A présent, celle-ci n'ajoute
l'individu qu'avec la méthode List.add() simple.
Ajouter au bon endroit directement avec une ArrayList aurait donné une complexité quadratique (au pire cas, on ajoute au début et tous les éléments doivent être décalés). Comme nous nous sommes de plus rendu compte qu'on n'ajoutait que très rarement un seul individu, mais plutôt plusieurs à chaque reproduction, nous avons pris le parti de faire ces ajouts très rapidement (en O(1) : ajout en fin d'ArrayList) puis d'appeler une seule fois à la fin de chaque série d'ajouts la méthode Collections.sort() afin d'obtenir une liste triée avec un algorithme de complexité O(n*log(n)) (QuickSort).
Dans la méthode de reproduction, on ajoute n individus. Pour ce
faire, on sélectionne n fois deux individus au hasard dans la
population puis on effectue un appel à méthode d'ajout de la façon
suivante : add(individu1.croisement(individu2)).
Concernant les choix des index des individus, un
petit ajout a été fait pour favoriser les véritables
croisements entre personnes différentes. Cette instruction est la
suivante : (par le biais de l'opérateur ternaire) si le second
index déterminé au hasard vaut le premier, on le modifie :
Index2 = ( Index1 == Index2 ) ;? (Index2 + 1)% taille de la
population : Index2
ce qui permet d'éviter de créer forcément un individu strictement
indentique à un autre déjà présent dans la liste (d'après la
propriété du croisement qui indique que deux individus indentiques
doivent donner le même individu).
L'une des méthodes très intéressantes dont nous sommes satisfaits d'avoir découvert et utilisé le principe pour ce projet est la méthode statique shuffle() qui permet de mélanger une liste d'entier en temps linéaire là où l'algorithme le plus courant est quadratique (on doit vérifier à chaque insertion d'un nombre que celui-ci n'est pas déjà présent dans la liste des nombres déjà insérés. Tant que c'est le cas, il faut tirer à nouveau un nombre.).
Par exemple, cette fonction est utilisée pour la génération d'un chemin dans le problème du voyageur de commerce ou pour le mélange des éléments de P dans le problème du sac à dos.
Cet algorithme est en plus très simple :
soit Random(x) une fonction qui renvoie un entier appartenant à [0;x-1]
soit tab le tableau à mélanger
Pour i de n-1 à 2
swapindex = Random(i)
échanger(tab[i], tab[swapindex])
Fin pour
getopt() en langage C en quelque
sorte.plus le score est élevé plus l'individu est adapté. Cette remarque peut paraître anodine mais elle ne l'est pas : un chemin est par exemple d'autant meilleur qu'il possède un faible coût. On prendra donc soin de ne pas créer le score avec le coût directement, mais de passer par une fonction inverse (pour les deux problèmes, nous avons par exemple utilisé x a pour image -x).
compare() de cette classe renvoie en fait simplement
le retour de la méthode compareTo() appelée sur le score de
chacun des individus (voir ci-dessus).La première partie ayant été implémentée, nous l'avons utilisée pour résoudre notre problème de parcours des villes.
Les villes sont numérotées de 0 à N-1. L'ensemble des villes et des routes les reliant est représenté par une matrice de N lignes par N colonnes contenant des entiers. Dans la matrice, sur la ligne i et à la colonne j, l'entier est la distance pour aller de la ville i à la ville j. L'absence de route entre deux villes est indiquée par le nombre de villes X la distance maximum d'une route reliant une ville à une autre directement. Cette valeur permet de savoir immédiatement si une route contient un chemin contient une transition invalide et est donc particulièrement utile pour les tests.
Nous avons donc écrit une classe GraphImpl implémentant l'interface Graph. Cette interface tente de standardiser les méthodes qui sont indispensables pour un graphe. De plus, si on désire créer une classe représentant un graphe avec des listes de suivants, cette méthode aura l'avantage de permettre d'interchanger de façon transparente les deux implémentations (si on n'a bien sûr pas ajouté dans une implémentation des méthodes qui soient inexistantes dans l'interface).
Pour pouvoir utiliser cette classe pour résoudre notre problème de parcours des villes avec l'algorithme génétique générique que nous avons implémenté dans la première partie, nous avons considéré qu'un chemin est un individu. Ainsi, nous avons écrit la classe Path implémentant l'interface Individu et représentant les chemins. Elle implémente principalement les méthodes de croisement et de mutation des individus.
Après comparaison de différentes méthodes de croisement, nous avons opté pour celle du croisement en deux points. Etant donné deux parcours, on en construit un autre selon le principe suivant :

| Score père ≥ Score mère | Score père < Score mère | |
|---|---|---|
| Intervalle ≥ moitié du nombre de sommets | Échange Père/Mère | Rien à faire |
| Intervalle < moitié du nombre de sommets | Rien à faire | Échange Père/Mère |



Il s'agit de modifier un des éléments constitutifs de la solution, ici c'est une ville. Quand un chemin doit être muté, on choisit aléatoirement deux index de villes, on intervertit les sommets correspondants. Cette méthode possède évidemment une complexité en O(1).
Schéma d'illustration :

La première classe que nous avons implémentée est ReadUserInput qui permet la saisie et le stockage des éléments de P dans un tableau (tabEltP) et du volume du sac à dos dans une variable (backPackVolume). La seconde classe créée est Fill qui contient principalement un tableau (tabIndexEltP) des indices des éléments de P dans le tableau tabEltP et une variable indexQ qui permet d'obtenir les éléments de Q.
Nous considérons qu'une organisation d'indices des éléments de P est un individu. C'est donc pour cette raison que la classe Fill implémente l'interface Individu. Cette dernière déclare 3 fonctions dont les fonctions de croisement et de mutation. La méthode de croisement de Fill est très proche de celle implémentée pour résoudre le problème du voyageur de commerce. Quant à la méthode de mutation, elle s'en inspire aussi beaucoup.
Pour une plus grande rapidité du programme, nous réalisons plusieurs tests
avant de lancer ou pas l'algorithme génétique. Ceux-ci sont destinés à
vérifier que le calcul ne va pas être lancé alors qu'il existe une solution
évidente et simple. Ils sont décrits par le schéma suivant : 


Une organisation d'indices des éléments de P dans tabEltP dans
tabIndexEltP est un individu. Pour générer ces différentes organisations
aléatoirement on utilise la méthode PopulationImpl.shuffle()
décrite précédemment.
La méthode utilisée est similaire à celle du voyageur de commerce :

Une fois l'individu obtenu, pour obtenir la liste des éléments de Q, on se sert de tabEltP, de tabIndexEltP et d'une variable nommée indexQ.
La reproduction précédente donne le tableau tabIndexEltP qui contient les indices 3 1 4 0 2 :
La variable indexQ, initialisée à 0, s'incrémente jusqu'à dépasser la valeur de backPackVolume (36). Soit 28+2+173>36, donc indexQ = 3. Au final, on décrémente indexQ de 1 (car l'indice de la 1ère case d'un tableau est toujours 0), donc elle vaut 2.
Il suffit de permuter un nombre dans tabIndexEltP qui a un indice
inférieur à indexQ et un autre qui a un indice supérieur ou égal à
indexQ :

Après chaque mutation, la variable indexQ est recalculée. Dans ce cas, elle vaut encore 2. Après une telle reproduction et une telle mutation, l'ensemble Q obtenu contient les éléments 28 1. S'afficheront donc à l'écran ces éléments.
L'utilisateur pourra, s'il le souhaite, saisir les paramètres suivants (cf :Mode d'emploi):
Une aide (-help) est fournie en cas de besoin.
Si l'utilisateur ne saisit aucun paramètre, le programme est lancé avec des paramètres par défaut.
Pour gérer les paramètres, nous avons implémenté la
classe abstraite Parameters qui se trouve dans le paquetage
Algogen. Nous l'avons fait hériter de deux classes :
Au préalable, il vous faut le logiciel springgraph. Pour l'installer sous Debian GNU/Linux : apt-get install springgraph.
La méthode genDotfile() génère une image donnant une représentation graphique simple (sans les valuations) d'une matrice des villes créée. Elle retourne une chaîne de caractères.
Il y a deux possibilités pour générer une telle représentation :
$cat nomfichier.dot|springgraph > nomfichier.png qui
génèrera le fichier nomfichier.png représentant le graphe....|springgraph > nomfichier.png.| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 90 | 10 | 90 | 12 |
| 1 | 5 | 90 | 10 | 90 |
| 2 | 17 | 90 | 90 | 90 |
| 3 | 90 | 90 | 90 | 90 |
Représentation graphique du graphe ci-dessus générée avec
springgraph :

Pour tester la partie de notre programme qui concerne le voyageur de commerce, nous avons saisi la matrice de configuration des villes et des routes (entrée en dur dans le constructeur sans paramètre) fournie dans l'énoncé du projet. Sur cette matrice de configuration, la meilleure solution a pour coût 30. Lors de nos tests, il nous est effectivement arrivé de parvenir à trouver ce résultat (et évidemment rien d'inférieur).
Ce résultat nous a donc permis de savoir que notre algorithme était (ou en tout paraissait) correct. Cela a donc été la méthode de validation principale pour cette partie.
Pour savoir si nos résultats étaient fiables, nous avons fait appel à un autre binôme. Avec ce binôme, nous avons lancé le programme avec un même ensemble P et un même entier naturel n. Nous avons le plus souvent trouvé des résultats indentiques ou très proches..
Eclipse possède un debugger intégré. Cette option, ainsi que la méthode
d'affichage System.out.println(..)
, nous ont permis de gagner du temps
pour repérer plus rapidement ce qui n'allait pas dans le programme.
Pour toutes les parties du projet, nous avons utilisé l'option Xprof de la machine virtuelle java, le profiler intégré (similaire à gprof par exemple). Nous avons ainsi pu analyser les parties à améliorer et éviter de passer inutilement du temps par exemple dans une méthode qui représenterait 0.1% du temps.
Exemple (extrait) d'affichage avec l'option Xprof :
Flat profile of 9.24 secs (270 total ticks): main
Compiled + native Method
14.9% 18 + 22 fr.umlv.boubakermathus.commerce.Path.croisement
13.4% 9 + 27 fr.umlv.boubakermathus.commerce.Path.mutation
11.6% 21 + 10 java.util.Arrays.mergeSort
10.4% 28 + 0 fr.umlv.boubakermathus.commerce.GraphImpl.pathCost
7.1% 19 + 0 fr.umlv.boubakermathus.algogen.IndividuComparator.compare
6.3% 17 + 0 fr.umlv.boubakermathus.commerce.GraphImpl.getDirectCost
4.9% 13 + 0 fr.umlv.boubakermathus.commerce.Path.fonctionne
4.1% 11 + 0 fr.umlv.boubakermathus.algogen.ScoreImpl.compareTo
3.0% 8 + 0 java.util.Random.setSeed
3.0% 8 + 0 java.util.Random.next
3.0% 8 + 0 java.util.ArrayList.RangeCheck
2.2% 6 + 0 java.util.ArrayList.set
1.9% 5 + 0 java.util.Collections.sort
1.9% 5 + 0 fr.umlv.boubakermathus.algogen.PopulationImpl.reproduction
1.5% 4 + 0 java.util.ArrayList.get
1.5% 4 + 0 java.util.Random.nextInt
0.7% 2 + 0 java.util.Random.nextDouble
0.7% 2 + 0 java.util.AbstractList$Itr.next
0.7% 2 + 0 java.util.AbstractList$ListItr.set
0.7% 1 + 1 fr.umlv.boubakermathus.algogen.PopulationImpl.mutation
0.4% 1 + 0 java.util.ArrayList.ensureCapacity
94.0% 192 + 60 Total compiled
Ici, on remarque évidemment que les méthodes dans lesquelles on passe le
plus de temps sont croisement() et mutation(), ce
qui est un résultat attendu. Avant de faire une amélioration significative,
nous voyions apparaître la méthode compare() en troisième
position avec environ 13 à 14% du temps total. C'est grâce à cela que nous
avons défini un objet IndividuComparator déclaré public static
final dans PopulationImpl que nous avons passé à la méthode
Collections.sort() (dans la méthode
PopulationImpl.sortPopulation()) au lieu de new
IndividuComparator() comme précédemment.
Nous avons fait de multiples essais en faisant varier différents paramètres pour observer l'impact de chacun de ces paramètres sur la "qualité" de la solution trouvée et le temps de calcul nécessaire.
Afin de déterminer ces paramètres, nous avons voulu voir l'évolution des courbes de progression des scores de la population.
Pour ce faire, nous avons décidé d'utiliser l'outil de génération de
graphiques gnuplot. Or il nous fallait tout d'abord générer les données à
fournir à celui-ci. Il nous a très vite semblé évident qu'il serait
impossible de changer manuellement les coefficients de reproduction, de
mutation et le nombre d'itérations pour faire tous les différents tests.
Nous avons donc écrit la méthode
Algogen.testValues() qui permet de générer automatiquement tous
ces fichiers selon les différents intervalles et les pas (steps)
spécifiés.
Après comparaison des courbes, nous avons donc décidé de fixer les paramètres suivants pour le voyageur de commerce :
Pour le sac à dos, nous avons choisi des paramètres identiques à ceux précédemment :
Voir les graphiques et les commentaires
JAVA est un Langage Orienté Objet (LOO). L' Orienté Objet signifie manipuler uniquement des objets c'est-à-dire des ensembles groupés de variables et de méthodes associées à des entités intégrant naturellement ces variables et ces méthodes.
L' OO présente plusieurs avantages : facilité d'organisation de classes, réutilisation, méthode plus intuitive, facilité de répartition du travail et de correction, projet plus facile à gérer. L'intérêt principal de l'OO réside dans le fait que l'on ne décrit plus par le code des actions à réaliser de façon linéaire mais par des ensembles cohérents appelés objets.
L' OO est facilement concevable car il décrit des entités comme il en
existe dans le monde réel. Ainsi, l'objet ScoreImpl qui implémente la méthode
ScoreImpl.compareTo() est facilement concevable et peut être
utilisé, par exemple, dans un jeu de combat où on fera interagir plusieurs
objets ScoreImpl. Les modèles à objets ont été créés pour modéliser le monde
réel. "Dans un modèle à objets, toute entité du monde réel est un objet, et
réciproquement, tout objet représente une entité du monde réel".
L' OO permet en quelque sorte de factoriser le code en ensembles logiques. Du point de vue de la programmation, l' OO nous a permis d'écrire du code facilement lisible de taille minimale et à la correction aisée.
Les informations concernant un domaine étant centralisées en objets, il est facile de sécuriser le programme en interdisant ou en autorisant l'accès à ces objets aux autres parties du programme.
L'algorithme présente une approche un peu brutale, nécessitant une grande
puissance de calcul (mais pour cela les ordinateurs contemporains sont
largement suffisants), mais présentant l'immense avantage pratique de fournir
des solutions pas trop éloignées de l'optimal, même si l'on ne connaît pas de
méthode de résolution. Par exemple, pour le problème du voyageur de commerce,
l'approche naïve est de calculer tous les itinéraires, puis de choisir le
plus court chemin reliant un certain nombre de villes données. Un calcul
rapide indique cependant que pour plus de quelques dizaines de villes, le
nombre de possibilités comporte des centaines de zéros ! La méthode
naïve est donc inutilisable pour des problèmes réalistes. La branche de la
technique qui cherche à résoudre ce genre de problème porte le nom de
«recherche opérationnelle». Contrairement à la recherche opérationnelle,
l'algorithme génétique n'exige aucune connaissance de la manière dont
résoudre le problème; il est seulement nécessaire de pouvoir évaluer la
qualité d'une solution. Il est également léger à mettre en oeuvre (le
moteur
est commun, il y a moins de programmation spécifique au
problème à faire).
Le seul reproche qu'on puisse faire aux algorithmes génétiques est qu'au vu de la part
de hasard à la base du principe, on ne peut pas garantir que la ou les solutions
trouvées soient les meilleures. On peut donc itérer indéfiniment jusqu'à estimer
que la solution est acceptable, mais définir cet acceptable
peut se
réveler délicat.
Le tableau suivant récapitule les différences entre une approche de recherche opérationnelle et la résolution du même problème par l'algorithme génétique :
| Recherche Opérationnelle (approche ad hoc, analytique, spécifique) | Approche génétique | |
|---|---|---|
| Rapidité | Selon solution, parfois bonne | Bonne à très bonne |
| Performance | Selon solution | Bonne |
| Compréhension du problème | Nécessaire | Non nécessaire |
| Travail humain | Très variable : de quelques jours à quelques thèses | Faible : Quelques jours ou semaines |
| Applicabilité | Faible : La plupart des problèmes intéressants n'ont pas d'expression mathématique exploitable, ou sont non calculables, ou "NP-complets" (trop de possibilités). | Générale |
| Etapes intermédiaires? | ne sont pas des solutions (il faut attendre la fin des calculs) | sont des solutions (le processus peut être interrompu à tout moment) |
Plus le problème est complexe, plus l'algorithme génétique montre sa supériorité.
Ce projet JAVA est l'aboutissement d'un trimestre d'enseignement de ce langage. La réalisation de ce projet fut, pour nous, une réelle source d'enrichissement. Il nous a permis d'approfondir nos connaissances concernant ce langage (classes, interfaces, javadoc ...) et la programmation Orienté Objet. Sur le plan relationnel, il a nous a permis de travailler en groupe, ce qui est important pour notre future vie professionnelle. Tout le travail demandé a été réalisé avec succès et nous nous en réjouissons.
Nous tenons de plus à remercier les professeurs pour ce sujet si intéressant et important pour notre culture générale informatique. En effet, plutôt que de nous avoir demandé de réaliser un projet uniquement destiné à nous apprendre le langage, nous avons aussi pu découvrir un des domaines de recherche informatique les plus mystérieux et passionnant.
Connaître des techniques de résolution de problèmes NP complets tels que les algorithmes génétiques ou le recuit simulé par exemple sont en effet des éléments non négligeables pour un informaticien.
Page valide XHTML 1.0 Strict.